ЗНО -2015 з математики демонстраційний варіант

ПОГЛИБЛЕНИЙ РІВЕНЬ ЗНО -2015 з математики демонстраційний варіант

Розв’яжіть завдання 31–34. Одержані числові відповіді запишіть у зошиті та бланку Б. Відповідь записуйте лише десятковим дробом, ураховуючи положення коми, по одній цифрі в кожній клітинці відповідно до зразків, наведених у бланку А.

31. Спростіть вираз  та обчисліть його значення, якщо x=-3.

Відповідь: 0,508

32.  Скільки всього різних парних п’ятицифрових чисел можна утворити з цифр 1, 2, 3, 4 та 5, якщо в кожному з цих чисел усі цифри різні?

Відповідь: 48

33. У кулю, радіус якої дорівнює 5 см, уписано циліндр. Визначте відношення об’єму циліндра до об’єму кулі, якщо радіус основи циліндра дорівнює 4 см. Відповідь запишіть десятковим дробом

Відповідь: 0,576

34. Обчисліть значення інтеграла .

Відповідь: 5

Розв’яжіть завдання 35, 36. Запишіть у бланку Б послідовні логічні дії та пояснення всіх етапів розв’язання завдань, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання завдань рисунками, графіками тощо.

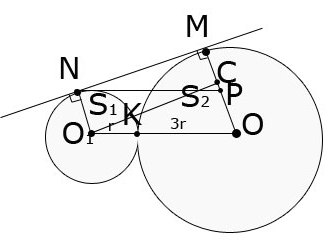
35. Два кола, радіуси яких дорівнюють r і 3r, дотикаються зовні в точці K. До цих кіл проведено спільну зовнішню дотичну MN (точка M належить більшому колу, точка N – меншому).

1. Доведіть, що центри цих кіл та точка їхнього дотику K лежать на одній прямій.

2. Обчисліть площу фігури KMN, обмеженої меншими дугами KМ і KN цих кіл та відрізком MN.

Розв’язання

Демонстраційний тест ЗНО 2015. Поглиблений рівень. Завдання 36

Проведемо пряму паралельну до OO_1.

Розглянемо ΔNMР (∠M=90)

NP²= NM²+ MP²

NM²= NP²- MP²;  NP= OO₁=4r; MP=OM-OP; MP=3r-r=2r;

NM²=16r²-4r²=12r²;

NM=2√3r ;

Розглянемо прямокутну трапецію NMOO₁

S_NMOO1=NM· (O₁N+OM)/2, де NM – висота трапеції;

S_NMOO1=((r+3r)/2)·2√3r=4√3 r²

S_NKM= S_NMOO1- S_NO1K- S_MOK

У трапеції провдемо пряму O₁С паралельну до NM.

Розглянемо Δ O₁СО (∠С=90⁰)

СО=2r

sin∠O= O₁C/ O₁O=2√3r/4r=√3/2;

∠O=60⁰

∠O₁=120⁰ (бо NPOO₁ – паралелограм);

S_NO1K= (π·O₁N²)/ 360⁰·∠O₁= ((π·r²)/ 360⁰)·120⁰=π/3·r²;

S_MOK=(π·OM²)/ 360⁰·∠O=((π·3r²)/ 360⁰)·60⁰=π/6·9r²= 3π/2·r²;

S_NKM=4√3 ·r²- π/3·r²- 3π/2·r²=(24√3 ·r²-2 π·r²)/6=(24√3 ·r²-11 π·r²)/6.

36. Розв’яжіть рівняння  залежно від значень параметра a.

Поглиблений рівень задача 36

Теги 2015відповідідемонстраційнийзноматематика